Матч 332, Квадраты (Squares)

Дивизион 2, Уровень 3

Имеется прямоугольное поле с квадратными ячейками. Каждая ячейка содержит заглавную букву латинского алфавита. Квадрат с вершинами в четырех ячейках считается действительным, если координаты всех четырех ячеек разные, и все они содержат одинаковую букву. Например, поле

ABA

BAB

ABA

содержит два действительных квадрата:

A.A
...
A.A

и

.B.
B.B
.B.

Поле задается массивом строк field. Необходимо найти количество действительных квадратов на поле. Два квадрата считаются разными, если у одного из них есть вершина, которой нет у другого.

Класс: Squares

Метод: int countSquares(vector<string> field)

Ограничения: field содержит от 1 до 50 символов, field[i] содержат одинаковое количество символов, 1 £ field[i] £ 50, каждый элемент field[i][j] содержит буквы ‘A’-‘Z’.

Вход. Массив строк field.

Выход. Количество квадратов на прямоугольном поле.

Пример входа

field

{"ABA", "BAB", "ABA"}

{"AA", "AA"}

{"AABCA", "AAAAA", "BAAAB", "AAAEA", "ADBFA"}

Пример выхода

2

1

11

РЕШЕНИЕ

перебор

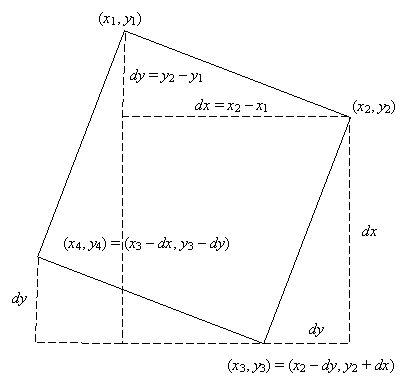
Перебираем координаты двух соседних углов квадрата (x₁, y₁) и (x₂, y₂). Если буквы, стоящие в них, равны, то вычисляем координаты двух других углов квадрата (x₃, y₃) и (x₄, y₄). Положив dx = x₂ – x₁ и dy = y₂ – y₁, получим что (x₃, y₃) = (x₂ – dy, y₂ + dx) и (x₄, y₄) = (x₃ – dx, y₃ – dy). Если координаты третьей и четвертой точки допустимы, а буквы, стоящие в них, совпадают с буквами в первой и второй точке, то обнаружен очередной квадрат. Общее количество найденных квадратов подсчитываем в переменной res.

ПРОГРАММА

#include <cstdio>

#include <vector>

#include <string>

using namespace std;

class Squares

{

public:

int countSquares(vector<string> field)

{

int x1, y1, x2, y2, x3, y3, x4, y4, dx, dy, res = 0;

int n = field.size(), m = field[0].size();

for(x1 = 0; x1 < n; x1++)

for(y1 = 0; y1 < m; y1++)

for(x2 = x1; x2 < n; x2++)

for(y2 = y1 + 1; y2 < m; y2++)

if (field[x1][y1] == field[x2][y2])

{

dy = y2 - y1; dx = x2 - x1;

y3 = y2 + dx; x3 = x2 - dy;

if (0 <= x3 && x3 < n && 0 <= y3 && y3 < m &&

field[x1][y1] == field[x3][y3])

{

y4 = y3 - dy; x4 = x3 - dx;

if (0 <= x4 && x4 < n && 0 <= y4 && y4 < m &&

field[x1][y1] == field[x4][y4]) res++;

}

}

return res;

}

};